Finite Size Fluctuations in Complex Systems : a Large Deviation Approach – CEFIPRA project

Co-PI: Shamik Gupta TIFR Mumbai

Participants: Rupak Majumder, Samir Sahoo, Anwar El Rhirhayi

Complex systems are usually modelled by a large number of coupled nonlinear Ordinary Differential Equations (ODEs) (or Stochastic Differential Equations -SDEs- if one takes ambient noise into account) involving the microscopic degrees of freedom. These equations, being nonlinear and coupled, are inevitably difficult to understand.

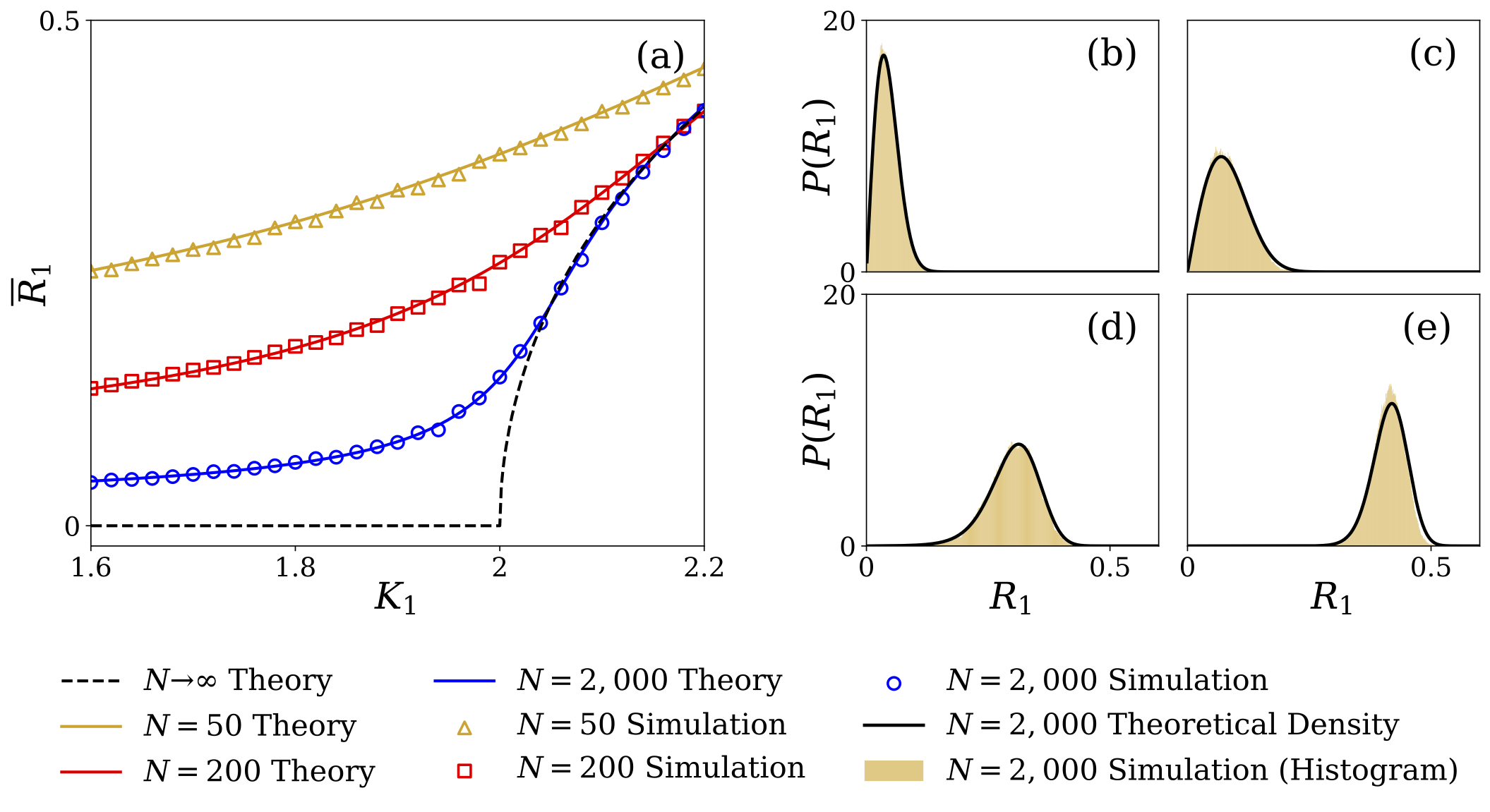
It is then a well established strategy to describe the system in terms of one- particle, two-particle, … distribution functions, and to write down deterministic partial differential equations (PDEs) of kinetic or diffusive type for their evolution, which are valid in some large N limit. These distribution functions depend on all the microscopic degrees of freedom (e.g., position, velocity, some internal degree of freedom…), and hence are often still difficult to handle. The next step is to reduce the description further, taking advantage of small parameters at hand: it may be a small Knudsen number in classical kinetic theory, a small inertia yielding an overdamped approximation, or, a situation which will be of particular interest to us, a small bifurcation parameter near an instability, underpinning a center manifold reduction. In many application fields, among them spontaneous synchronization which will be a motivating example in the project, it is crucial to go beyond this infinite N, deterministic picture, and to account for finite-N fluctuations.

Illustration (joint work with Rupak Majumder and Shamik Gupta, 2025): combining center manifold expansion with Dean-Kawasaki equation to capture finite size fluctuations for a synchronization model.