Results

We have studied the classical dynamics of a hydrogen atom in perpendicular magnetic and electric fields with methods of perturbation theory initially developed in Celestial Mechanics. Being a perturbed Kepler problem, the Hamiltonian can be studied with different sets of action-angle variables, each of them having advantages and disadvantages:

• Delaunay variables: these action-angle variables were introduced by Delaunay to develop systematically perturbation theory in the problem of the Moon. They have a direct geometric interpretation in terms of the Kepler ellipse: action variables are related to semi-major axis, eccentricity and inclination of the orbit, while angle variables are the longitude of node, argument of perihelion and mean anomaly of the "planet". The inconvenient of these variables is that the eccentricity is not a constant of motion of the Stark effect.
• "Electric action-angle variables": we gave this name to another set of action-angle variables, originally introduced by Born, starting from parabolic variables. Two actions are the same as Delaunay actions, but a third action is introduced which corresponds to the electric quantum number. The advantage is that the Stark Hamiltonian depends only on the action variables, which greatly simplifies perturbation theory. The drawback is that these variables are more difficult to handle in computations, and don't have such an obvious geometric interpretation.

To combine the advantages of both sets of variables, we have established simple transformation formulae between them (perturbatively in the electric field). We then wrote the crossed-fields Hamiltonian in electric action-angle variables, and computed its average with respect to the fastest variable (describing the position of the electron on the Kepler ellipse). We thus obtained a two-degrees-of-freedom Hamiltonian and studied its periodic orbits in different regimes. The geometry of these orbits is then easily interpreted by translating into Delaunay variables.

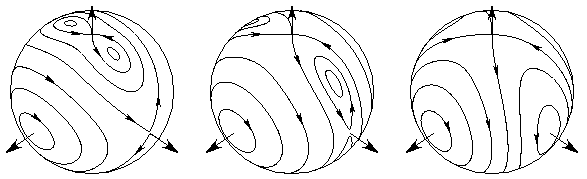
Phase portraits of an approximation to the crossed-fields Hamiltonian obtained by double-averaging, represented for increasing values of the ratio (magnetic field)/(electric field). The vertical coordinate is the angular momentum projected on the electric field, while the longitude is its conjugate variable, which is related to the longitude of node. The poles correspond to a periodic orbit of the Stark Hamiltonian. The point on the equator which changes form hyperbolic to elliptic represents orbits in the plane perpendicular to the magnetic field. The elliptic point near the equator represents a more complicated, three-dimensional orbit.

Poincaré sections of an approximation to the crossed-fields Hamiltonian obtained by single-averaging, for similar parameter values as above, and the same coordinates.