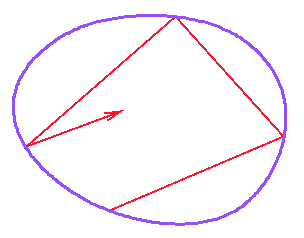
Consider the free classical motion of a particle in a plane domain, making elastic collisions with the walls of this domain. This is the simplest possible version of the "billiard ball problem", considered by George D. Birkhoff around 1927, when he was working on the theory of dynamical systems, extending ideas by Henri Poincaré.
A billiard can be described by its bouncing map, which specifies the evolution of position and velocity from one collision with the boundary to the next one. Depending on the shape of the boundary, this simple system may exhibit very different behaviours. While the billiard in a circle is integrable, and the billiard in a stadium is ergodic, it seems that for a generic boundary, it displays periodic, quasi-periodic and chaotic orbits at the same time.
Various generalisations of the problem have been considered since Birkhoff's work, for instance billiards in higher dimensions, with force fields, time-dependent boundaries, or boundaries replaced by a smooth potential.
We have considered planar billiards in a perpendicular magnetic field, and an in-plane potential. The main aspects of our work on billiards are summarised in this proceedings.

The billiard in a circle is integrable.
The billiard in a stadium is ergodic and mixing.