Introduction

Metastability in physics

Examples of metastable systems include supercooled liquids, suspersaturated gases and wronly magnetised ferromagnets. In all these cases, the system is close to a first-order phase transition line, but on the "wrong" side. Such a situation can be achieved by "quenching" a system initially in thermodynamic equilibrium. In the new, non-equilibrium state, the system's free energy needs to overcome a potential barrier in order to reach the new equilibrium state (frozen water, condensed gas, rightly magnetised ferromagnet), a transition which may require a very long time. Until the equilibrium state is reached, the system is thus in a metastable state.

Metastability in stochastic lattice systems

Mathematically rigorous results on metastability exist in particular for stochastic lattice systems, such as the Ising model with Glauber dynamics, or the lattice gas with Kawasaki dynamics. Consider for instance an Ising model at low temperature, in the "minus" phase (almost all spins equal to -1), but put in a weak, positive magnetic field. It is then more favourable for the system to be in the "plus" phase. However, to reach such a state, the system has to flip (almost) all its spins, thereby creating interfaces which are energetically unfavourable. The most economic transition path consists in creating a "droplet of plus in a sea of minus", which ultimately invades all space. There exist very precise results on the shape of the critical droplet, on the way it grows, and on the time required for the transition.

Metastability in reversible diffusions

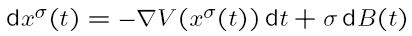
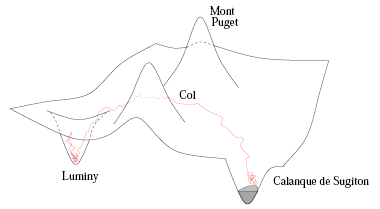
where V is a (confining) potential, and B(t) is a standard Brownian motion (if the drift term does not derive from a potential, such systems may also display metastability, but the results are less explicit). If the potential has several local minima (potential wells), the dynamics for small noise intensity 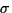resembles a Markovian jump process between small neighbouhoods of local minima, with transition times exponentially long in the potential difference to be overcome.

Metastability in spatially extended reversible diffusions

With Barbara Gentz and Bastien Fernandez, I am working on metastability in stochastic lattice systems with continuous on-site variables, described by systems of interacting stochastic differential equations. First results are contained in this and this paper. We have considered the effect of bifucations on the Eyring-Kramers formula in this paper.

In his thesis, Sébastien Dutercq analyses the effect of symmetries on the Eyring-Kramers law. First results on jump processes are contained in this paper. An application to a particle system with a conservation law can be found here.

Metastability in stochastic partial differential equations

With Barbara Gentz, I have proved an analogue of Kramers' law for parabolic stochastic partial differential equations (SPDEs) of Allen-Cahn type, of the form

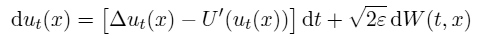
where U is a bistable potential and W(t,x) denotes space-time white noise. Detailed results are contained in this paper, and formal computations can be found here.

With Giacomo Di Gesù and Hendrik Weber, I have extended this result to Allen-Cahn equations on the 2-dimensional torus (when the torus is small enough for the identically zero solution to be the transition state). A renormalisation procedure is required for the equation and the Eyring-Kramers prefactor to be well-defined. The results are contained in this paper.

Simulation of a 2D stochastic Allen-Cahn equation with conserved magnetisation:

Home