Variables aléatoires réelles à densité

$\begin{example} On laisse tomber une aiguille \\lq a tricoter. La probabilit\'e qu'... ... dit que $\alpha$\ suit la \defwd{loi uniforme}\/ sur $[0,2\pi]$. \end{example}$

D'une manière générale, si la probabilité qu'une variable aléatoire

appartienne à un intervalle peut s'écrire comme l'intégrale d'une fonction

sur cet intervalle, on dira que cette variable aléatoire admet la densité

$\begin{definition}[Densit\'e] Une fonction $f: \R\to[0,\infty[$, int\'egrable se... ...quation} \int_{-\infty}^{\infty} f(x)\,\6x = 1\;. \end{equation}\end{definition}$

$\begin{example} % latex2html id marker 1799 \hfill \begin{enum} \item Densit\'e ... ...on} f(x) = \frac c\pi \frac1{x^2+c^2}\;. \end{equation} \end{enum}\end{example}$

$\begin{figure}{\small {\bf Figure 2.1. } Densit\'es et fonctions de r\'epartiti... ... exponentielle $\cE\!xp(1)$, (c) loi de Cauchy de param\\lq etre $1$.}\end{figure}$

$\begin{definition}[Fonction de r\'epartition] Une fonction $F: \R\to[0,1]$\ est ... ...in{equation} F(x) = \int_{-\infty}^x f(y)\,\6y\;. \end{equation}\end{definition}$

On a les propriétés suivantes:
$\begin{enum} \item Si $f$\ est une densit\'e, la fonction $F$\ d\'efinie par~\eq... ...tre-exemples, faisant intervenir, par exemple, des objets fractals). \end{enum}$

Le lien entre la notion de fonction de répartition et les variables aléatoires vient du fait que pour toute variable aléatoire réelle, $\prob{X\leqs t}$ est une fonction de répartition. En effet,
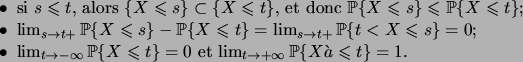
$\begin{itemiz} \item si $s\leqs t$, alors $\set{X\leqs s} \subset \set{X\leqs t}... ...fty}\prob{X\leqs t}=0$\ et $\lim_{t\to+\infty}\prob{Xà\leqs t}=1$. \end{itemiz}$
Ceci motive la définition suivante.

$\begin{definition}[Variable al\'eatoire \\lq a densit\'e] Si $X$\ est une variable ... ...ns ce cas, on peut remplacer $<$\ par $\leqs$\ et inversement. \end{definition}$

$\begin{example} % latex2html id marker 1913 \hfill \begin{enum} \item Soit $(\Om... ...loi g\'eom\'etrique, cf. la Proposition~\ref{prop_va1}. \end{enum}\end{example}$

Pour des variables aléatoires admettant une densité, l'espérance et la variance se définissent de manière analogue au cas discret, en remplaçant les sommes par des intégrales.

$\begin{definition}[Esp\'erance et variance] Soit $X$\ une variable al\'eatoire a... ...ty}^\infty (x-\expec{X})^2 f(x)\,\6x\;. \end{equation}\end{enum}\end{definition}$

$\begin{example}\hfill \begin{enum} \item \emph{Loi normale standard}\/: On a \b... ...e tent\'e de consid\'erer son esp\'erance comme nulle). \end{enum}\end{example}$

$\begin{definition}[Fonction g\'en\'eratrice] Soit $X$\ une variable al\'eatoire ... ...z x} f(x)\,\6x \equiv \bigexpec{\e^{\icx z X}}\;. \end{equation}\end{definition}$

$\displaystyle \abs{G_X(z)} \leqs \int_{-\infty}^\infty \abs{\e^{\icx z x}} f(x)\,\6x = 1\;,$

(2.1)

$\displaystyle G_X'(z) = \icx \int_{-\infty}^\infty x\e^{\icx z x} f(x)\,\6x\;,$

(2.2)

$\displaystyle G_X'(0) = \icx \expec{X}\;,\qquad G_X''(0) = -\expec{X^2}\;.$

(2.3)

$\begin{example}\hfill \begin{enum} \item \emph{Loi exponentielle de param\\lq etre ... ...e quantit\'e \'etant souvent d\'enot\'ee $(2\ell-1)!!$. \end{enum}\end{example}$