



Next: Le processus ponctuel de
Up: Introduction aux processus stochastiques
Previous: Introduction aux processus stochastiques
Contents
La marche aléatoire unidimensionnelle symétrique
Considérons une expérience de Pile ou Face. Pour  jets successifs, on
peut prendre comme univers le produit
jets successifs, on
peut prendre comme univers le produit
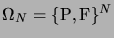 .
Considérons alors la variable aléatoire
.
Considérons alors la variable aléatoire 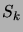 égale à la
différence entre le nombre de Pile et de Face obtenus lors des
égale à la
différence entre le nombre de Pile et de Face obtenus lors des 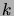 premiers jets. On peut écrire
premiers jets. On peut écrire
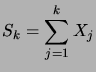 où où  |
(3.1) |
La marche aléatoire unidimensionnelle symétrique est la suite
des 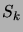 obtenue dans le cas
obtenue dans le cas
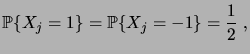 |
(3.2) |
les 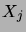 étant supposés indépendants. Les réalisations
du processus sont des suites
étant supposés indépendants. Les réalisations
du processus sont des suites
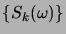 d'entiers telles que
d'entiers telles que
 et
et
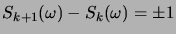 (fig_marche1). La probabilité de chaque suite de longueur
(fig_marche1). La probabilité de chaque suite de longueur 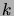 est
est 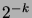 .
.
Commençons par établir quelques propriétés élémentaires de la
variable aléatoire 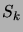 .
.
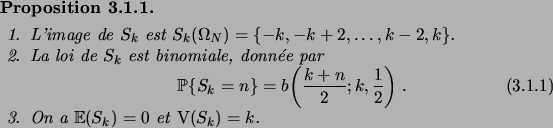
D´EMONSTRATION.


La Proposition 3.1.1 implique que 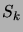 est nul en moyenne, mais
que ses fluctuations sont d'ordre
est nul en moyenne, mais
que ses fluctuations sont d'ordre 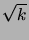 .
En particulier, la probabilité que le processus se trouve en 0 au
.
En particulier, la probabilité que le processus se trouve en 0 au
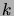 -ème pas est donnée par
-ème pas est donnée par
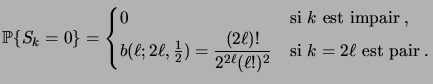 |
(3.3) |
Remarquons que la formule de Stirling implique que pour 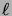 grand,
grand,
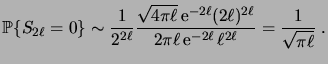 |
(3.4) |
Cependant, la loi de chaque 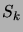 ne détermine pas le processus, les
ne détermine pas le processus, les
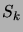 n'étant pas indépendants. Voici d'abord quelques propriétés
simples du processus considéré dans son ensemble:
n'étant pas indépendants. Voici d'abord quelques propriétés
simples du processus considéré dans son ensemble:
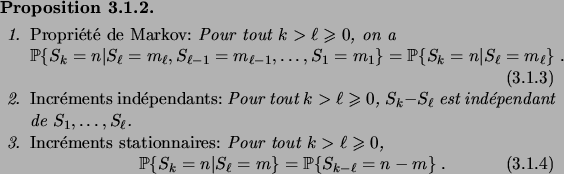
D´EMONSTRATION.
Nous pouvons décomposer
 |
(3.5) |
L'indépendance des
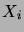
implique que
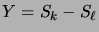
est indépendante
de

, donc aussi de

. Il suit que
Par le même raisonnement, nous avons également
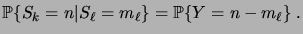 |
(3.7) |
Finalement,
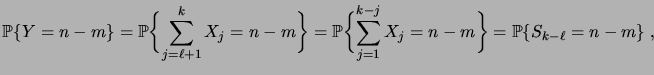 |
(3.8) |
du fait que les
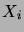
sont identiquement distribués.

La propriété de Markov signifie que l'évolution du
processus ne dépend que de son état présent, indépendamment de son
passé. Elle permet d'écrire des relations du genre
Voyons maintenant comment déduire de ces propriétés des informations
non triviales sur les réalisations du processus. Une première
quantité intéressante est le temps  du premier retour du
processus en 0 (fig_marche2):
du premier retour du
processus en 0 (fig_marche2):
 |
(3.9) |
Par exemple, dans l'expérience de jet de pièce de monnaie,  est le
nombre de fois que l'on jette la pièce jusqu'à obtenir pour la
première fois autant de Pile que de Face. Quelle est la loi de
est le
nombre de fois que l'on jette la pièce jusqu'à obtenir pour la
première fois autant de Pile que de Face. Quelle est la loi de  ?
Il est clair que
?
Il est clair que  ne peut
prendre que des valeurs paires. De plus, si
ne peut
prendre que des valeurs paires. De plus, si  alors
alors 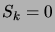 , donc
, donc
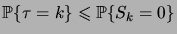 . En fait, il nous faut déterminer
. En fait, il nous faut déterminer
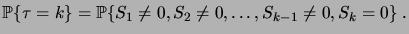 |
(3.10) |
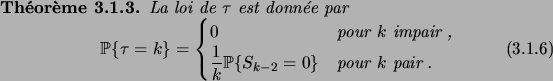
D´EMONSTRATION.
Supposons que

.
Comme le processus ne peut pas changer de signe sans passer par 0, on a
où nous avons utilisé la propriété de Markov dans la dernière
ligne. La propriété des incréments stationnaires
implique
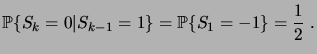 |
(3.12) |
Il suit que
Nous utilisons maintenant un argument important, appelé le
principe de réflexion: A tout chemin allant de
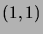
à

passant par 0, on peut faire correspondre un unique chemin de
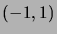
à

, obtenu en réfléchissant par rapport à l'axe
des abscisses la partie du chemin antérieure au premier passage en 0.
On a donc
 |
(3.14) |
Finalement, en appliquant de nouveau la propriété des incréments
stationnaires, on voit que
En remplaçant dans (
3.1.19), il vient
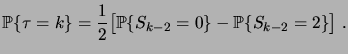 |
(3.16) |
Le reste de la preuve est un calcul direct. Comme
 |
(3.17) |
on obtient
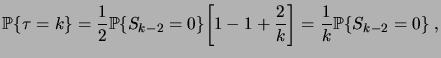 |
(3.18) |
ce qui conclut la démonstration.

Le tableau suivant donne les premières valeurs de la loi de  :
:
Il est donc assez probable de revenir rapidement en 0, puis la loi prend
des valeurs plutôt faibles, tout en décroissant lentement. Il suit
de (3.1.6) que pour des grands 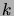 ,
,
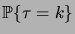 décroît comme
décroît comme
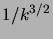 . Ce fait a une conséquence surprenante:
. Ce fait a une conséquence surprenante:
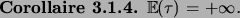
D´EMONSTRATION.
On a
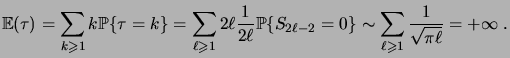 |
(3.19) |

En d'autres termes, la marche aléatoire finit toujours par revenir en 0,
mais la loi de  décroît trop lentement pour que son espérance
soit finie. Cela est lié au fait que si la marche aléatoire s'éloigne
beaucoup de 0, il lui faut longtemps pour y revenir.
décroît trop lentement pour que son espérance
soit finie. Cela est lié au fait que si la marche aléatoire s'éloigne
beaucoup de 0, il lui faut longtemps pour y revenir.
Considérons une autre application du principe de réflexion. Supposons
qu'une machine à sous fonctionne avec une mise d'un euro, et que la
machine rende soit deux euros, soit rien, avec la même probabilité.
Combien de fois peut-on jouer, si l'on possède initialement  euros?
La somme que l'on possède après avoir joué
euros?
La somme que l'on possède après avoir joué 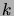 fois est égale à
fois est égale à
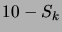 , on peut donc jouer jusqu'à ce que
, on peut donc jouer jusqu'à ce que  . Il nous faut donc
déterminer la loi de
. Il nous faut donc
déterminer la loi de
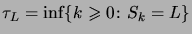 |
(3.20) |
pour  dans notre exemple.
dans notre exemple.

D´EMONSTRATION.
Considérons le cas
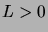
. On a
Invoquons alors à nouveau le principe de réflexion
(fig_marche4). A chaque réalisation telle que
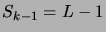
, qui
a déjà atteint le niveau
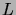
auparavant, on peut associer une
réalisation telle que
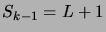
. Nous avons donc
Le cas
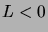
suit par symétrie.

Pour des raisons similaires à celles du cas du retour en 0, la loi de
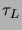 décroît en
décroît en 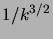 , et son espérance est donc infinie.
On est donc sûr de perdre tôt ou tard, tout en pouvant espérer jouer
infiniment longtemps. Le tableau suivant donne les premières valeurs de la
loi dans le cas
, et son espérance est donc infinie.
On est donc sûr de perdre tôt ou tard, tout en pouvant espérer jouer
infiniment longtemps. Le tableau suivant donne les premières valeurs de la
loi dans le cas  , donc si on ne possède que deux euros au début. On
constate que si l'on ne perd pas lors des
, donc si on ne possède que deux euros au début. On
constate que si l'on ne perd pas lors des 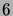 premiers coups, la
probabilité de perdre en
premiers coups, la
probabilité de perdre en 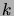 coups change très peu d'un
coups change très peu d'un 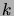 au suivant.
au suivant.




Next: Le processus ponctuel de
Up: Introduction aux processus stochastiques
Previous: Introduction aux processus stochastiques
Contents
berglund
2005-11-28
![]() jets successifs, on
peut prendre comme univers le produit
jets successifs, on
peut prendre comme univers le produit
![]() .
Considérons alors la variable aléatoire
.
Considérons alors la variable aléatoire ![]() égale à la
différence entre le nombre de Pile et de Face obtenus lors des
égale à la
différence entre le nombre de Pile et de Face obtenus lors des ![]() premiers jets. On peut écrire
premiers jets. On peut écrire
![]() .
.
![]() est nul en moyenne, mais
que ses fluctuations sont d'ordre
est nul en moyenne, mais
que ses fluctuations sont d'ordre ![]() .
En particulier, la probabilité que le processus se trouve en 0 au
.
En particulier, la probabilité que le processus se trouve en 0 au
![]() -ème pas est donnée par
-ème pas est donnée par
![]() ne détermine pas le processus, les
ne détermine pas le processus, les
![]() n'étant pas indépendants. Voici d'abord quelques propriétés
simples du processus considéré dans son ensemble:
n'étant pas indépendants. Voici d'abord quelques propriétés
simples du processus considéré dans son ensemble:
![]() du premier retour du
processus en 0 (fig_marche2):
du premier retour du
processus en 0 (fig_marche2):
![]() :
:
![]() décroît trop lentement pour que son espérance
soit finie. Cela est lié au fait que si la marche aléatoire s'éloigne
beaucoup de 0, il lui faut longtemps pour y revenir.
décroît trop lentement pour que son espérance
soit finie. Cela est lié au fait que si la marche aléatoire s'éloigne
beaucoup de 0, il lui faut longtemps pour y revenir.
![]() euros?
La somme que l'on possède après avoir joué
euros?
La somme que l'on possède après avoir joué ![]() fois est égale à
fois est égale à
![]() , on peut donc jouer jusqu'à ce que
, on peut donc jouer jusqu'à ce que ![]() . Il nous faut donc
déterminer la loi de
. Il nous faut donc
déterminer la loi de
![]() décroît en
décroît en ![]() , et son espérance est donc infinie.
On est donc sûr de perdre tôt ou tard, tout en pouvant espérer jouer
infiniment longtemps. Le tableau suivant donne les premières valeurs de la
loi dans le cas
, et son espérance est donc infinie.
On est donc sûr de perdre tôt ou tard, tout en pouvant espérer jouer
infiniment longtemps. Le tableau suivant donne les premières valeurs de la
loi dans le cas ![]() , donc si on ne possède que deux euros au début. On
constate que si l'on ne perd pas lors des
, donc si on ne possède que deux euros au début. On
constate que si l'on ne perd pas lors des ![]() premiers coups, la
probabilité de perdre en
premiers coups, la
probabilité de perdre en ![]() coups change très peu d'un
coups change très peu d'un ![]() au suivant.
au suivant.