Matthieu Astorg
Click on images for a higher resolution.
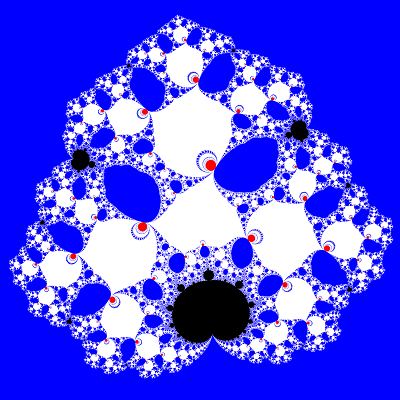
Mandelbrot set (very high resolution)



Slices of wandering domains for polynomial skew-products


Bifurcations in 1D families of quadratic skew-products


Parameter spaces of families of transcendental meromorphic maps


Parameter space of generalized horn maps (finite type maps)

Per1 slices in the cubic family

Small applet on sensibility to initial conditions for angle-doubling map
Click here











